El cálculo diferencial es una rama fundamental de las matemáticas que permite analizar el cambio de una cantidad con respecto a otra. Aunque puede parecer abstracto en un primer momento, sus aplicaciones prácticas abarcan desde la física hasta la economía, pasando por la biología, la ingeniería y la informática. Comprender el cálculo diferencial no solo facilita el estudio de fenómenos dinámicos, sino que también desarrolla habilidades analíticas esenciales.
¿Qué es el cálculo diferencial?
Definición y concepto central
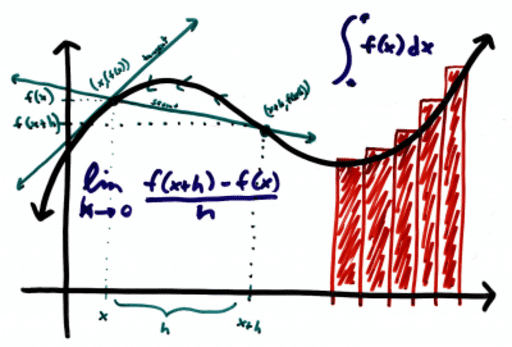
El cálculo diferencial se encarga del estudio de la variación de funciones. En términos simples, busca responder preguntas como: ¿cómo cambia una variable cuando otra cambia?, o ¿cuál es la tasa de cambio en un punto específico? Para responderlas, utiliza una herramienta clave: la derivada.
Una derivada mide cómo cambia una función en un instante determinado. Si bien esta idea puede parecer abstracta al principio, es la base para entender movimientos, optimizar recursos o analizar crecimiento y decrecimiento en sistemas reales.
Relación con el cálculo integral
Aunque son ramas distintas, el cálculo diferencial y el cálculo integral están íntimamente relacionados. Ambos conforman el cálculo como disciplina matemática. Mientras el diferencial estudia el cambio, el integral se enfoca en la acumulación. Juntos forman una herramienta poderosa para modelar y comprender el mundo que nos rodea.
Herramientas principales del cálculo diferencial
Funciones y límites
Para aplicar el cálculo diferencial, primero se deben comprender los conceptos de funciones y límites. Una función relaciona dos variables, mientras que un límite permite analizar qué sucede con la función cuando nos acercamos a cierto valor. Estos dos conceptos son la base para definir una derivada de forma rigurosa.
Por ejemplo, si queremos saber la velocidad instantánea de un objeto en movimiento, calculamos el límite del cociente de cambio a medida que el tiempo tiende a cero. Esta operación conduce directamente al concepto de derivada.
La derivada: significado e interpretación
La derivada de una función en un punto representa la pendiente de la recta tangente a la curva en ese punto. En otras palabras, indica la velocidad de cambio instantánea. Si la derivada es positiva, la función está creciendo; si es negativa, está decreciendo.
Además, la derivada tiene múltiples interpretaciones según el contexto. En física, representa velocidad o aceleración. En economía, puede indicar el cambio en el costo o ingreso marginal. Gracias a esta versatilidad, se ha convertido en una herramienta central en numerosos campos.
Reglas de derivación
Para facilitar los cálculos, existen reglas generales como la regla del producto, la regla del cociente y la regla de la cadena. Estas reglas permiten derivar funciones complejas sin necesidad de aplicar directamente el concepto de límite en cada caso.
Por ejemplo, si se conoce la derivada de funciones básicas como xnx^n, sin(x)\sin(x), ln(x)\ln(x), entre otras, se puede derivar casi cualquier función con relativa facilidad utilizando estas reglas.
Aplicaciones del cálculo diferencial
En la física
Uno de los campos donde el cálculo diferencial tiene mayor presencia es la física. Permite describir fenómenos como el movimiento, la velocidad, la aceleración, y las trayectorias de objetos. Sin él, no sería posible construir modelos que expliquen cómo interactúan las fuerzas en el universo.
Por ejemplo, para calcular la trayectoria de un proyectil o el comportamiento de un objeto bajo la influencia de la gravedad, es necesario aplicar derivadas. Incluso en campos más avanzados, como la relatividad o la mecánica cuántica, el cálculo diferencial es indispensable.
En la economía
El cálculo diferencial también se utiliza ampliamente en economía para analizar funciones de producción, maximizar beneficios o minimizar costos. La derivada ayuda a identificar puntos críticos donde ocurren máximos o mínimos, lo que permite tomar decisiones óptimas.
Además, al estudiar tendencias en precios o demanda, los economistas aplican el concepto de tasa de cambio para prever el comportamiento del mercado. Así, el cálculo diferencial se convierte en una herramienta clave para la toma de decisiones estratégicas.
En la biología y medicina
Aunque menos evidente, el cálculo diferencial también se aplica en biología y medicina. Se utiliza para modelar el crecimiento poblacional, analizar la propagación de enfermedades o estudiar procesos fisiológicos como la circulación sanguínea.
Gracias a su capacidad para describir cambios continuos, permite entender fenómenos complejos en organismos vivos. Por ejemplo, en la farmacología, se pueden modelar las tasas de absorción de medicamentos en el cuerpo mediante ecuaciones diferenciales.
La importancia de aprender cálculo diferencial
Desarrollo del pensamiento lógico
Más allá de sus aplicaciones prácticas, estudiar cálculo diferencial fomenta el desarrollo del pensamiento lógico y analítico. Resolver problemas, aplicar teoremas y entender conceptos abstractos son actividades que fortalecen habilidades mentales útiles en múltiples áreas de la vida y el trabajo.
Además, el cálculo diferencial ayuda a mejorar la capacidad para enfrentar desafíos complejos, pues enseña a descomponer problemas grandes en partes más simples, facilitando su análisis y solución.
Base para estudios avanzados
El cálculo diferencial es una base indispensable para seguir carreras en ciencia, tecnología, ingeniería o matemáticas. Incluso en informática y análisis de datos, entender cómo cambian los valores en una función puede marcar la diferencia entre un análisis superficial y uno profundo.
Asimismo, en áreas como la inteligencia artificial o la simulación computacional, muchas técnicas se construyen sobre conceptos derivados del cálculo. Por eso, dominar esta herramienta abre la puerta a campos innovadores y altamente demandados.
Conclusión
El cálculo diferencial es mucho más que una materia escolar: es una herramienta esencial para comprender, modelar y predecir el comportamiento de sistemas en constante cambio. Desde los movimientos de los planetas hasta las decisiones financieras, sus aplicaciones son tan diversas como profundas.
Aunque puede parecer complejo al principio, con práctica y paciencia se convierte en una herramienta poderosa y versátil. Entender el cálculo diferencial no solo permite resolver problemas matemáticos, sino también interpretar mejor el mundo que nos rodea.