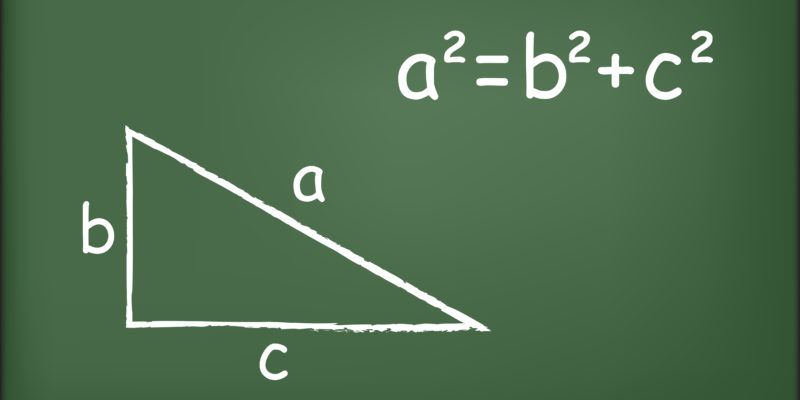La geometría ha sido una parte esencial del conocimiento humano durante siglos. Además, permite comprender las formas, tamaños y relaciones espaciales de los objetos. Dentro de esta disciplina, el teorema de Pitágoras ocupa un lugar central, ya que establece una relación exacta entre los lados de un triángulo rectángulo. Por lo tanto, es una herramienta fundamental para estudiantes, profesionales y aficionados a las matemáticas.
¿Qué es el teorema de Pitágoras?
El teorema de Pitágoras establece que, en un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos. En otras palabras, si se llaman aa y bb a los catetos y cc a la hipotenusa, se cumple que a2+b2=c2a^2 + b^2 = c^2. Además, esta relación permite calcular longitudes desconocidas siempre que se conozcan dos lados del triángulo.
Historia y origen del teorema de Pitágoras
Recibe su nombre del matemático griego Pitágoras, quien vivió alrededor del año 500 a.C. Sin embargo, registros históricos indican que civilizaciones como la egipcia y la babilónica ya conocían principios similares. Por consiguiente, el teorema se consolidó gracias a la sistematización de Pitágoras y su escuela, estableciendo una base formal para la geometría.
Componentes del teorema de Pitágoras
Comprender los elementos del teorema de Pitágoras es esencial para aplicarlo correctamente. Además, permite identificar rápidamente los lados de un triángulo rectángulo y resolver problemas prácticos de manera efectiva.
Hipotenusa
La hipotenusa es el lado más largo del triángulo rectángulo y se encuentra opuesto al ángulo recto. Por lo tanto, representa la diagonal que conecta los extremos de los catetos. Asimismo, su medida puede calcularse directamente usando los catetos gracias al teorema.
Catetos
Los catetos son los lados que forman el ángulo recto. Además, son perpendiculares entre sí y, combinados con la hipotenusa, completan la relación matemática que define el teorema. Por consiguiente, conocer al menos dos lados permite determinar el tercero de manera sencilla.
Aplicaciones del teorema de Pitágoras
El teorema de Pitágoras tiene múltiples aplicaciones en matemáticas, ingeniería y la vida cotidiana. En consecuencia, su estudio es fundamental tanto en la educación como en profesiones técnicas.
Geometría y trigonometría
En geometría, el teorema de Pitágoras permite calcular distancias y áreas de figuras planas. Además, sirve de base para conceptos más avanzados en trigonometría, como el cálculo de longitudes y ángulos en triángulos no rectángulos. Por lo tanto, se utiliza constantemente en problemas académicos y científicos.
Arquitectura y construcción
En arquitectura y construcción, el teorema de Pitágoras ayuda a diseñar estructuras rectas y precisas. Asimismo, se utiliza para medir diagonales, determinar alturas y asegurar que los ángulos rectos sean exactos. Por consiguiente, es indispensable para garantizar estabilidad y precisión en proyectos constructivos.
Vida cotidiana
El teorema de Pitágoras también se aplica en situaciones cotidianas. Por ejemplo, calcular la distancia entre dos puntos en un terreno, la longitud de una escalera o la altura de un objeto inaccesible. De este modo, permite resolver problemas prácticos de manera rápida y eficiente.
Demostraciones del teorema de Pitágoras
Existen numerosas demostraciones del teorema de Pitágoras, lo que refleja su importancia y versatilidad. Además, algunas son geométricas, mientras que otras emplean álgebra. En consecuencia, estudiar distintas demostraciones fortalece la comprensión del concepto y su aplicación.
Demostración geométrica
Una demostración clásica consiste en construir cuadrados sobre los lados de un triángulo rectángulo y demostrar que el área del cuadrado de la hipotenusa es igual a la suma de las áreas de los cuadrados de los catetos. Además, este enfoque visual ayuda a entender la relación de manera intuitiva.
Demostración algebraica
Otra demostración se basa en aplicar propiedades algebraicas de los números y operaciones con cuadrados. Por lo tanto, permite comprobar la validez del teorema sin recurrir a figuras geométricas. Asimismo, este método es útil en problemas más abstractos y en matemáticas avanzadas.
Importancia del teorema
El teorema de Pitágoras no solo es un principio matemático, sino también una herramienta esencial para el desarrollo del pensamiento lógico y analítico. Además, fomenta habilidades de razonamiento crítico y resolución de problemas.
Educación y formación matemática
El estudio del teorema de Pitágoras es obligatorio en la educación básica y secundaria. Por lo tanto, permite que los estudiantes comprendan relaciones espaciales y matemáticas fundamentales. Asimismo, facilita la transición hacia conceptos más complejos en geometría, trigonometría y física.
Ciencia y tecnología
En ciencia y tecnología, se aplica en mediciones precisas, diseño de experimentos y cálculo de distancias en distintos contextos. En consecuencia, constituye un elemento clave para ingenieros, arquitectos y científicos.
Resumiendo, el teorema de Pitágoras es una piedra angular de la geometría y las matemáticas. Además, su aplicación práctica abarca desde la educación hasta la arquitectura, la ingeniería y la vida diaria. Por consiguiente, comprender y utilizar este teorema es fundamental para resolver problemas, desarrollar pensamiento lógico y explorar el mundo que nos rodea de manera más precisa y científica.